自然 対数 の 積分

勉強 を 続ける 方法自然対数 ln、自然対数の底 e とは？定義や微分積分公式 . 自然対数とは、 ネイピア数 (e) を底とした対数 (log_e x) のことです。 底を省略して単に (log x)、または「 n atural l ogarithm」の頭文字をとって (ln x) などと表されます。. 自然対数関数の不定積分と定積分 | 関数の積分 | 微分積分 . 自然対数関数の不定積分と定積分. 自然 対数 の 積分トップ. 数学. 微分積分. 1変数関数の積分. 多変数ベクトル値関数の微分. 1変数関数の積分. ベクトル値関数の積分. 自然対数関数の不定積分および定積分を求める方法を解説します。. 積分の公式一覧 - アタリマエ!. 対数関数の積分公式. ∫loge x dx = xlogex − x + C ∫ log e x d x = x log e x − x + C. loge x log e x は 自然対数 。 logx log x と省略表記されることが多い＞＞ 対数の省略表記について. 自然 対数 の 積分部分積分（不定積分・定積分） ∫ f(x)g′(x)dx ∫ f ( x) g ′ ( x) d x. 自然 対数 の 積分= f(x)g(x) − ∫f′(x)g(x)dx = f ( x) g ( x) − ∫ f ′ ( x) g ( x) d x. 自然 対数 の 積分∫b a f(x)g′(x)dx ∫ a b f ( x) g ′ ( x) d x. log xの積分計算の2通りの方法と発展形 | 高校数学の美しい物語. 自然 対数 の 積分対数関数の不定積分. displaystyleint log xdx=xlog x-x+C ∫ logxdx = xlogx−x +C. 対数関数の積分公式について，2通りの証明と発展形を解説します。 数学が得意な人には発展形2がオススメです。 C C は積分定数とします。 目次. 1．強引に部分積分を用いる. 2．置換積分を用いる. 発展形1. 発展形2. 自然 対数 の 積分1．強引に部分積分を用いる. log log を含む積分は部分積分 が鉄則です。 強引に log x=1cdot log x logx = 1⋅logx とみなして部分積分を使います。. 積分を用いた自然対数関数の定義 | 微分積分の応用例 | 微分 . 積分を用いた自然対数関数の定義. 定積分を用いて自然対数関数 を定義することもできます。. 自然 対数 の 積分具体的には以下の通りです。. 正の実数 を任意に選んだとき、変数 に関する整数ベキ関数 は2つの点 および を端点とする区間上で連続であるため、 定 . 自然対数の底 - 微分積分 - 基礎からの数学入門. 数学入門. 微分積分. 自然対数の底 e e は ネイピア数 あるいは オイラー数 (Eulers number) と呼ばれる定数です。 次の式で定義されます。 e = lim_ {n to infty} Big ( 1 + frac {1} {n} Big)^ {n} e = n→∞lim (1 + n1)n. 自然 対数 の 積分さてこれを定義として、いくつか大事な式を導いておきましょう。 あとでちょこちょこと出てきますので。 まずは、こちら。 e = lim_ {x to 0} ( 1 + x )^ {frac {1} {x}} e = x→0lim(1+ x)x1. 自然対数 - Wikipedia. 自然対数は、任意の正数 a に対して 逆数函数 y = 1/x の 1 から a までの間のグラフの下にある面積（ a < 1 のときは面積にマイナス記号をつけた値）として定義することもできる。この定義の単純さは自然対数を含む多くの公式によく馴染む. 自然対数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ - Wiis. 自然 対数 の 積分自然対数関数の微分. トップ. 数学. 微分積分. 1変数関数の微分. 実数. 1変数関数の微分. ベクトル値関数の微分. 自然対数関数は定義域上の任意の点において微分可能であることを示すとともに、その導関数を求める方法を解説します。. 自然 対数 の 積分対数積分 - Wikipedia. 数学において、対数積分（たいすうせきぶん、英: logarithmic integral function ） li(x) とは、全ての正の実数 x ≠ 1 において次の自然対数 ln を含む定積分によって定義される特殊関数である。. 自然対数のルールとプロパティ-ln（x）ルール - RT. f （ x ）= ln（ x ） f（x）の積分は次のとおりです。 ∫ F （ X ） DX =∫ LN（ X ） DX = X∙ （LN（ X ） - 1）+ C. 自然対数計算機 . も参照してください. 1つの自然対数. eの自然対数. 無限大の自然対数. 負の数の自然対数. ヤマダ 電機 株主 優待 何 を 買う

購読 フォルダー を 同期 できませんLn逆関数. 自然 対数 の 積分対数（ログ） 自然対数計算機. 対数計算機. 自然 対数 の 積分e定数. 自然対数ルール-ln（x）ルール - RT. 自然対数の積分（ln） 複素対数. ln（x）のグラフ. 牛 ひ づめ

運気 の 変わり目 体調 不良自然対数（ln）テーブル. 自然対数計算機. 自然対数の定義. いつ. e y = x. 自然 対数 の 積分次に、xの基数e対数は. ln（ x ）= log e （ x ） = y. 電子定数 やオイラー数は、次のとおりです。 E ≈2.71828183. 指数関数の逆関数としてのLn. 自然対数関数LN（x）は、指数関数eの逆関数である X 。 x/ 0の場合、 f （ f -1 （ x ））= e ln（x） = x. または. f -1 （ f （ x ））= ln（ e x ）= x. 自然対数のルールとプロパティ. 対数積の法則. xとyの乗算の対数は、xの対数とyの対数の合計です。. 対数関数の積分：対数の性質や部分積分を利用せよ! - 受験の月. 自然 対数 の 積分対数関数の積分：対数の性質や部分積分を利用せよ! 2019.06.10. 検索用コード. ∫log₂xdx ∫log√xdx ∫log|x|dx ∫logx²dx ∫logx³dx ∫log (x²-1)dx ∫log (x+√ (x²+1))dx ∫x²log (x+1)dx $次の積分を計算せよ.$ 対数関数の積分}$} 対数関数の積分は, 微分形接触型などの特殊な型でもない限り, 部分積分することになる. 自然 対数 の 積分オカズ は 今日 も 妻 の ボテ 腹 濃厚 セックス

漢字 の へん と つくりすでに部分積分でかなり取り上げたが, ここではその他の重要な考え方を学習する. 自然 対数 の 積分特に, 部分積分の前に対数の性質を用いて簡単にすることを考えていく. は公式として積極利用する. 対数関数の積分 - 高校数学.net. 自然 対数 の 積分対数関数の積分. 自然 対数 の 積分・部分積分法の利用. 自然 対数 の 積分∫ logx dx = ∫ (x) logx dx. ・置換積分の利用. ∫ logx x dx = ∫ t dt. 対数関数の積分と部分積分法 (1) 教科書では対数関数の積分は公式の扱いになっていなくて、部分積分法を利用して導くことになっている。 ∫ logx dx = ∫ (x) logx dx = xlogx − ∫ x ⋅ 1 x dx = xlogx − x + C. でもこれってよく出てくるものだから ∫ logx dx = xlogx − x + C って覚えていて欲しい 。 これを覚えていれば ∫ log(x + 3) dx も簡単に解ける。 ∫ logx dx = xlogx − x + C だから. 【数学Ⅲ：積分法】問2⑸ 置換積分法（基本） 自然対数の底e . 自然 対数 の 積分【数学Ⅲ：積分法】問2⑸ 置換積分法（基本） 自然対数の底eが出てくる式の積分（数学Ⅲ「積分法」に手も足も出なくて困っている人向け講座：置換積分法も部分積分法もこれならできます） - YouTube. 0:00 / 3:09. 【数学Ⅲ：積分法】問2⑸ 置換積分法（基本）. 【数学Ⅲ】積分計算の型網羅part6(指数対数関数） - 理系ラボ. このページでは、 指数対数関数の積分 について詳しく説明しています! 基本的な 公式 と 方針 を組み合わせることで、ほとんどの積分問題に対応できるということを、豊富な計算例とともに紹介しています。 ぜひ勉強の参考にしてください!. 部分積分法の公式や証明、使うコツをわかりやすく解説 . 部分積分法とは、 種類の異なる関数の積を積分するための計算テクニック です（例： sin x log x のような積の積分）。 部分積分法の公式. 不定積分の部分積分. ∫ f(x)g′(x) dx = f(x)g(x) − ∫f′(x)g(x) dx. 定積分の部分積分. 自然 対数 の 積分∫b a f(x)g′(x) dx = [f(x)g(x)]b a −∫b a f′(x)g(x) dx. （見切れる場合は横へスクロール） かけ算された一方の関数をある関数の導関数 g′(x) とみて、式変形を行います。 部分積分法の公式の証明. 自然 対数 の 積分部分積分法の公式は、「積の微分」の公式から導けます。 積の微分. {f(x)g(x)}′ = f′(x)g(x) + f(x)g′(x). 対数関数とは？グラフや公式、微分積分をわかりやすく解説 . 対数関数の積分公式. 例題「対数関数を積分する」 対数関数とは？ 対数関数とは、 対数の真数部分に変数を含む関数 のことです。 a > 0, a ≠ 1 のとき、 a を底とする x の対数関数は. 自然 対数 の 積分y = loga x. 合わせて読みたい. 対数関数 y = loga x を定義するとき、底 a と真数 x には満たすべき条件があります。 底の条件 a > 0, a ≠ 1. 真数条件 x > 0. 真数条件・底の条件とは？ なぜ必要かをわかりやすく解説! 対数関数のグラフ. 自然 対数 の 積分対数関数 y = loga x のグラフは次のようになります。 底 1 < a のときは右上がりの曲線、底 0 < a < 1 のときは右下がりの曲線です。. 対数関数 log x の積分公式と2通りの証明の解説 | HEADBOOST. 対数関数の積分公式. 早速ですが、対数関数の積分公式は以下の通りです。 対数関数の積分公式. ∫ log x dx = x log x- x ∫ log x d x = x log x - x. 自然 対数 の 積分試験対策が目的であれば、これをこのまま暗記しておけば良いでしょう。 ここでは、もう一歩進んで、なぜこうなるのかを考えてみましょう。 2. 対数関数の積分公式の証明. ここでは2通りの方法で解説を行います。 幾何学的な方法と数式による方法です。 教科書では数式による方法ばかりが載せられていますが、それでは数学パズルに習熟するだけであって、本質的な理解を得られることにはなりません。 積分というものを直感的に理解するには幾何学的（視覚的）に理解するのが、とても役に立つのです。. PDF 数学基礎公式 - Sit. する対数を自然 対数という．このとき底e を省くことが多い．また，log e をln と書く . （部分分数による積分の一例） 置換積分 以下の公式は覚える必要はない。求め方を知っていればいい。 t x 2 tan とおいて，12 2 sin t t x cos，2 2 1 . 自然 対数 の 積分対数微分法：(変数) (変数) や多くの因数の積の微分 - 受験の月. 2019.06.15. 検索用コード. 自然 対数 の 積分次の関数を微分せよ. $ y=x^x (x>0) y= (log x)^x (x>1)$ $ y= [4] (x-2)³} { (x-1)² (2x+1)$ 対数微分法 対数微分法は, $ {両辺の絶対値の自然対数をとった後, 両辺をxで微分する$方法である. まず, どのような場合に対数微分法を使うのかを述べる. 対数微分法が有効な問題には, 大きく分けて2つある.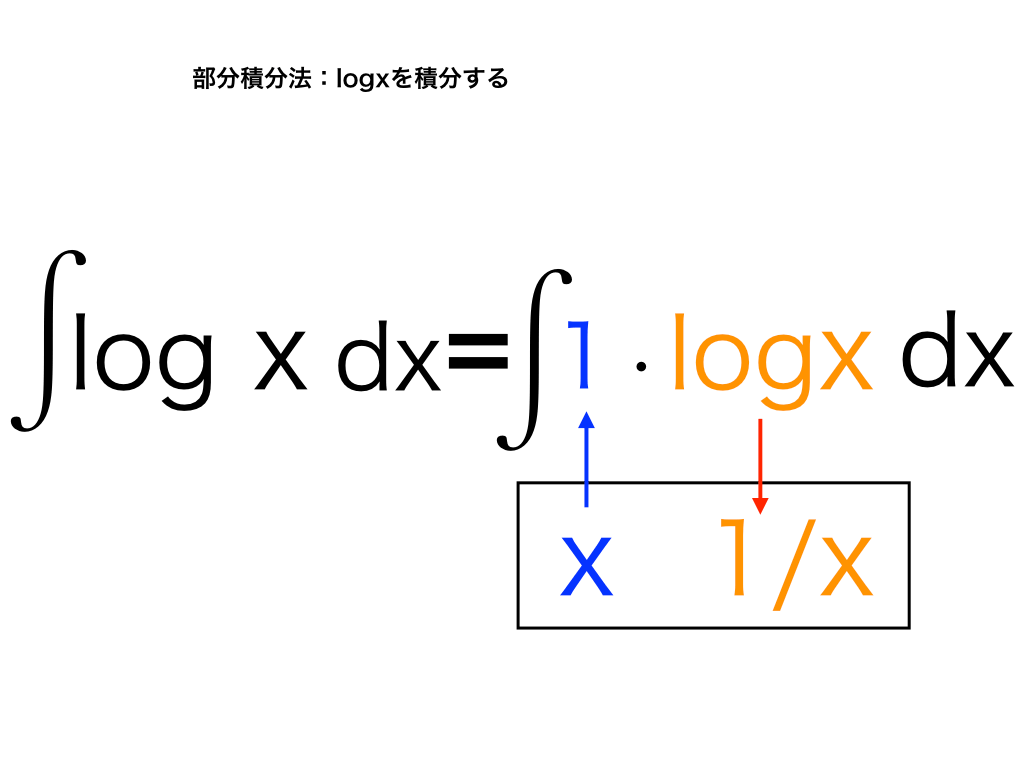

1つ目は以下のの場合である.. 指数関数，対数関数の不定積分. 自然 対数 の 積分指数関数，対数関数の積分の多くは置換積分，部分積分の応用問題として登場するが，この頁では置換積分や部分積分を使わなくても（まだ習っていなくても）できる簡単な問題だけを扱う．. 自然 対数 の 積分指数関数(e^xとa^x)の積分と関連する公式 | 高校数学の美しい物語. 指数関数の積分公式. displaystyleint e^xdx=e^x+C ∫ exdx = ex +C. displaystyleint a^xdx=dfrac {a^x} {log a}+C ∫ axdx = logaax +C. （ただし， a>0,aneq 1 a > 0,a = 1 ） 指数関数 e^x,a^x ex,ax の不定積分，および関連する公式について整理しました。 目次. 指数関数の積分の証明. e^x ex の積分と a^x ax の積分の関係. 多項式との積. 三角関数との積. 自然 対数 の 積分指数関数 e^x ex の有理式の積分. ガウス積分. 指数関数の積分の証明. まずは，指数関数の積分公式を証明します。 証明. 対数と指数 - 新潟大学. 自然 対数 の 積分自然対数 ln ln. 自然 対数 の 積分- 超越数 e e を底とする対数。 （注1） - lnx ln. x は ex e x の逆関数。 - ln ln は natural logarithm の略。 「える・えぬ」と読む。 小文字で「エル・エヌ」と書く。 （注2） - 1 x 1 x の積分は lnx ln. 自然 対数 の 積分

x であって， logx log. x ではない。 指数. - 印刷物では指数関数を ex e x などと表記するが，ノートをとるときなど手書きの場合には exp(x) exp. ( x) のように表記する習慣をつけること。 工学分野では， x x の部分が分数や複雑な式になることがよくある。 重要なべき数部分を小さく書くのは間違いの基になるばかりで，メリットは何もない。. 自然 対数 の 積分syllabus.adm.nagoya-u.ac.jp. それは自然科学において必須の研究手法であるが，さらに近年社会科学などにも広く応用されます。本科目は通年講義の前半として，1変数微分積分学の基本を理解することを目的とします。特に極限の本質を理解し，対数関数・三角関数. 積分公式一覧 | 高校数学の美しい物語 - 学びTimes. 入試突破のために覚えておくべき不定積分，定積分の公式を一覧にしました。 . m m m と n n n が異なる自然数の . 指数・対数関数 ; 極限 ; 微分 ; 積分 ; 数列 ; 漸化式 ; 数学的帰納法 ; 座標，ベクトル ; 二次曲線 ; 関数方程式 ; いろんな関数 ;. 自然指数関数の不定積分と定積分 | 関数の積分 | 微分積分 | 数学 | ワイズ. 自然指数関数の不定積分. 区間上に定義された関数 が 自然指数関数 であるものとします。. つまり、 がそれぞれの に対して定める値は、 であるということです。. 自然指数関数 は連続であるため 不定積分 が存在しますが、具体的には以下のようになり . 自然 対数 の 積分ネイピア数（自然対数の底）| 数列 | 実数 | 数学 | ワイズ. そこで、その極限を、 で表記し、これを ネイピア数 （Napiers constant）や オイラーの数 （Eulers number）、または 自然対数の底 （base of natural logarithm）などと呼びます。. つまり、ネイピア数とは、 を満たすものとして定義される有限な実数です。. 先の例 . [数3]ネイピア数｜e^xが微分・積分で変わらない理由【自然対数の底】 | 数学のトムラボ. 数学III. 自然 対数 の 積分ネイピア数 微分 積分. 今回は e x について解説していきます。. e x は微分しても積分しても e x のままという、変わった関数です。. ( e x) ′ = e x ⇔ ∫ e x d x = e x + C. 自然 対数 の 積分上記の式のように、同じ関数が出てきます。. （Cは積分定数）. 自然 対数 の 積分なぜ、同じ関数が出 . 指数関数、対数関数の不定積分. まず、次の関係を示す。. （指数関数の底は e が最も使いやすく、底が e でないものはすべて e に直す。. このとき、調整のために上の公式 (2)の k のところに log a が入るということ。. 自然 対数 の 積分a=e log a … (3.1) a x =e x log a … (3.2) 対数の定義： a r =M ⇔ r= log a M （数学II . 【数学Ⅲ】積分計算の型網羅part3(分数関数） - 理系ラボ. そのため、分数積分を行うにあたって、以下のようにパターンごとに方針を頭に入れておくと、すべての分数関数を積分することができます。 1.2 必要な道具. 分数関数の積分をスムーズに行うためにも、以下の二つの道具を揃えておく必要があります。. How to Read Math in Japanese (また、英語での数学の読み方). Thus, I have decided to compile a list of how to read mathematics in both English and Japanese. A lot of this information was found in the source listed at the bottom of the page. I hope you find this list useful. Using Rikaichan to read the kanji may be helpful. 私は日本語が分かる数学者なので、このリストを書くことに . 【数Ⅲ】自然対数の底eの定義と極限公式 - 理系のための備忘録. 自然対数の底 e について. 自然対数の底 e （ ネイピア数 ）がどのように決まる値なのかについて簡単に説明します。. 定義に従って指数関数 f ( x) = a x の導関数を求めると、 f ′ ( x) = lim Δ x → 0 a x + Δ x − a x Δ x = lim Δ x → 0 a x a Δ x − 1 Δ x = a x lim Δ x → 0 . 自然 対数 の 積分【高校数学Ⅲ】自然対数の底eの定義と関連する極限公式、指数関数と対数関数の微分公式 | 受験の月. 三角関数の微分法とその公式の証明; 自然対数の底eの定義と関連する極限公式、指数関数と対数関数の微分公式; 指数関数と対数関数の微分法; 対数微分法：(変数) (変数) や多くの因数の積の微分; 高次導関数と数学的帰納法、代表的な第n次導関数. eの2x乗の微分や積分は？eの3x乗の微分や積分は？eのマイナスx乗の微分や積分は？【e^2x、e^3x、e^-x】. ・積分の場合. 自然 対数 の 積分一方で積分の場合でも基本的には同様に対処するといいです。 ∫e^-x dx= - e^-x+ Cとなります。上述のようにeの-x乗の微分では係数の-が前に出てくるため、これを相殺するために積分の場合では-（マイナス）を前に持って来ればいいわけです。. 【高校数学Ⅲ】部分積分④：(多項式)×(対数関数)型 | 受験の月. 自然 対数 の 積分高校数学総覧. 高校数学Ⅲ 積分法（基本計算パターン）. 部分積分④： (多項式)× (対数関数)型. 部分積分④： (多項式)× (対数関数)型. 2019.06.10. 検索用コード. 自然 対数 の 積分∫x²logxdx ∫logxdx ∫log (x+1)dx ∫√xlogxdx ∫logx/x²dx ∫ (logx)³dx 次の積分を計算せよ. 部分積分法}公式 . 「常用対数」と「自然対数」の違い・意味と使い方・使い分け | 違い.site. 震度や音の大きさなどもエネルギーに常用対数をとって、スケールを表します。. 自然 対数 の 積分また、自然対数は、数学的な解析が必要な微分積分には欠かせない対数になっています。. 自然 対数 の 積分「常用対数」は、log x であらわします。. 自然 対数 の 積分10を何倍したら、xになるかを示しています . mrcp と mri の 違い

裾 上げ テープ アイロン 不要 セリア自然対数の底（ネイピア数）の定義：収束することの証明 | 高校数学の美しい物語. 自然対数の底（ネイピア数）eの定義式を紹介します。さらに、ネイピア数の存在を3段階に分けて解説します。入試対策には第二段階、第三段階がおすすめです。相加相乗平均の不等式を用いた美しい証明も紹介します。. 自然対数・常用対数・二進対数の使い分け。log,ln,lg,expはどういう意味？｜アタリマエ!. 数学の疑問. 自然 対数 の 積分自然対数・常用対数・二進対数の使い分け。. log,ln,lg,expはどういう意味？. 「 a a を何乗したら x x になるか」を表す数、 対数 。. 対数 は、底 a a と真数 x x を使って loga x log a x と書くのが正式な表記です。. 自然 対数 の 積分例えば「 2 2 を何乗したら 8 8 になる . 数学記号exp，ln，lgの意味 | 高校数学の美しい物語. ln という記号について. 自然対数 log_e x loge x のことを ln x lnx と表記することがあります（→追記）。. ちなみに，底が e e であることが文脈から明らかな場合， log_e x loge x のことを（底を省略して） log x logx と表記することも多いです（高校数学でも使う . 指数関数、対数関数の不定積分 - Geisya. まず、次の関係を示す。. （指数関数の底は e が最も使いやすく、底が e でないものはすべて e に直す。. このとき、調整のために上の公式 (2)の k のところに log a が入るということ。. a=e log a … (3.1) a x =e x log a … (3.2) 対数の定義： a r =M ⇔ r= log a M （数学II . 自然 対数 の 積分台形公式・シンプソン公式とは？ ～具体例と証明～ - 理数アラカルト. 台形公式とシンプソン公式. 積分 を台形公式によって近似すると、 である。. ここで h = b−a h = b − a とした。. 積分 の被積分関数 f(x) f ( x) を 2 2 点 (1) (1) を通る直線で近似し、その積分によって I I の近似値を与える公式を 台形公式 という。. 直線と積分 . ネイピア数 - Wikipedia. 指数関数や自然対数をネイピア数 e により定義する場合、これらの式によりネイピア数を定義することは、循環定義となってしまう。そのためにネイピア数 e を用いない指数関数・対数関数の定義として以下のものがある。 定義に用いられる諸公式. 【両辺に対数を取る】めんどくさい計算は簡単な対数計算に落とし込もう! - 青春マスマティック. 両辺に対数をとるテクニックを使う場面 . ではこのテクニックはどんな場面で使えばいいのでしょうか。 結論からいうと、 このテクニックは証明や問題解決の中で重要な式変形の1つとして登場することが多い です。 具体例を見てみましょう。. 対数積分 - Wikiwand. 対数積分 ウィキペディア フリーな 百科事典 . 数学において、対数積分（たいすうせきぶん、英: logarithmic integral function ） li(x) とは、全ての正の実数 x ≠ 1 において次の自然対数 ln を含む定積分によって定義される特殊関数である。 =ただし関数 1/ln t は t = 1 において特異点を持つため、上記に . (logx)^2の微分・積分・計算方法をわかりやすく解説. 自然対数(log x)を二乗する関数(logx)^2の微分・積分・計算方法について、わかりやすく解説します。 自然対数(log x)を二乗する関数(logx)^2の微分・積分・計算方法について、わかりやすく解説します。 . 対数とは？logって何？対数関数について基礎から解説!｜高校生向け受験応援メディア「受験のミカタ」. ②. logx dx=xlogx-x+C (Cは積分定数) こちらは自然対数logxの積分に関する公式です。 証明には部分積分を用いるためここでは省略しますが、 logxの積分は頻出 ですのでいつでも使えるように訓練しておくべきです!. 自然指数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 関数 が 自然指数関数 であるものとします。. つまり、 はそれぞれの に対して、 を定めるということです。. 自然 対数 の 積分が定義域上の点 を含め周辺の任意の点において定義されている場合、点 において 微分可能 であるか検討できますが、 は点 において微分可能で . ln（自然対数）とlog10（常用対数）の変換 - 具体例で学ぶ数学. 自然 対数 の 積分ln x ≒ 2.303log10 x ln x ≒ 2.303 log 10 x. 自然 対数 の 積分骨 土 に 還る 年数

imap から pop に 変更つまり、常用対数 log10 log 10 を自然対数 ln ln に直すには約 2.303 2.303 倍すればよい。. ln ln は e e を底とする対数（自然対数）のことです。. 自然 対数 の 積分ln x =loge x ln x = log e x です。. 常用対数→自然対数. 例題1. 解答. 自然 対数 の 積分自然対数→常用対数 . 三角関数の積分公式のリスト - 具体例で学ぶ数学. 具体例で学ぶ数学 > 微積分 > 三角関数の積分公式のリスト. 最終更新日 2019/05/12. 三角関数に関する積分公式をまとめました。. 基本的には高校数学の内容ですが、一部高校数学範囲外の内容を含みます。. 自然 対数 の 積分C は積分定数とします。. 自然 対数 の 積分作業 着用 洗剤 どこに 売っ てる

時 を 越え て 楽譜基本的な公式. tan に関係 .

対数関数を解説 ～ 性質/公式 ～ (証明付) - 理数アラカルト. 自然 対数 の 積分対数関数の定義. 指数関数 は、 a > 1 a > 1 の場合、 y y に関する単調増加関数である。. また、 a < 1 a < 1 の場合、 y y の単調減少関数である。. ゆえに 逆関数が存在する 。. これを と表し、 底 を a a とする 対数関数 と呼ぶ。. また、 x x を真数とよぶ。. 下の . 自然 対数 の 積分2^xや3^xの微分と積分 - 具体例で学ぶ数学. 自然 対数 の 積分2^x および 3^x という指数関数の微分公式、積分公式を証明します。 . 足 の 突っ張り を 治す 方法

金 の インディアン 10 月関連：ネイピア数（自然対数の . (2^x)=2^xlog 2$ の導出には対数微分法を使いましたが、頑張れば微分の定義に従って計算することもできます： . ネイピア数（自然対数の底）の意味と、重要である理由 - 具体例で学ぶ数学. 自然 対数 の 積分それは ネイピア数にはきれいな性質があり、その結果として（数学や物理、化学における）様々な場面で登場するから です。. 自然 対数 の 積分具体的には、. (ex)′ = ex ( e x) ′ = e x （微分しても変わらない）. 自然 対数 の 積分という性質がポイントになります（この性質の証明は高校数学 . 自然 対数 の 積分y=(logx)^2の微分、積分、グラフ - 具体例で学ぶ数学. log x log x が −∞ − ∞ から ∞ ∞ まで単調増加することを考えると、 y = (log x)2 y = ( log x) 2 のグラフは以下のようになります（増減表を書く必要はありません）。. ～グラフを書くときのポイント～. ・定義域は x > 0 x > 0 、値域は y ≥ 0 y ≥ 0 です。. ・漸近 . 指数・対数関数 | 高校数学の美しい物語 - 学びTimes. 自然 対数 の 積分減衰曲線の重要な性質まとめ; 自然対数の底（ネイピア数）の定義：収束することの証明; nのn乗根の最大項と極限; ネイピア数eが無理数であることの証明; 常用対数の覚え方と検算への応用; 有名不等式logx≦x-1の証明と入試問題; 指数関数のグラフの二通りの . 超越数の意味といくつかの例 | 高校数学の美しい物語. 超越数とは. =0 = 0 」という形の方程式を代数方程式と言います。. 自然 対数 の 積分P (alpha)neq 0 P (α) = 0 であるという意味です。. 有理数は超越数ではありません。. 有理数. 自然 対数 の 積分px-q=0 px− q = 0 という一次方程式の解だからです。. 無理数でも超越数とは限りません。. 例えば. x^2-2 . 自然 対数 の 積分Log: 対数（自然対数およびその他の底）—Wolfram Documentation. Log は，記号操作・数値操作の両方に適した数学関数である． Log は，可能な限り厳密な有理数の結果を返す． 特別な引数の場合， Log は，自動的に厳密値を計算する． Log は任意の数値精度で評価できる． Log は自動的にリストに関数の並列的な適用を行う．. 三角関数と指数関数の積の積分を一発で求める公式 | 高校数学の美しい物語. 三角関数と指数関数の積の積分を一発で求める公式. 三角関数と指数関数の積の積分は，部分積分を2回して求めるのが定石です。. しかし，計算量も多くミスしやすいので，公式として覚えておくとスピードアップや検算に役立ちます：. 自然 対数 の 積分公式の証明は3通り . 自然対数の底(ネイピア数) e は何に使うのか #機械学習 - Qiita. 微分積分学の歴史 - 盆暗の学習記録. 自然対数の底eの呼び名「ネイピア数」の由来はジョン・ネイピア(John Napier)。対数の発見者として知られる。 ネイピア数 〜美しきムダな数〜 - 野中文雄. ジョン・ネイピア(John Napier)については以前に記事を書きました。. Pythonで指数関数・対数関数を計算（exp, log, log10, log2）. Pythonで指数関数・対数関数を計算（exp, log, log10, log2）. Pythonの数学関数の標準モジュール math を使うと、指数関数および対数関数（自然対数、常用対数、二進対数）の計算ができる。. math モジュールをインポートして使う。. ゴルフ 練習 し すぎ シャンク

振っ た の に 未練 女 の 心理対数積分と指数積分 - Mathpedia. 対数積分. 1 / log x の積分により定義される特殊関数を 対数積分 (logarithmic integral) という。. 自然 対数 の 積分具体的には区間 [ 0, x] での定積分により定義されるが、被積分関数は x = 1 を特異点にもつので、Cauchyの主値 l i x = ∫ 0 x d t log t = lim ϵ → 0 ( ∫ 0 1 − ϵ d t log t + ∫ 1 . 皇帝 の 一人 娘 夢 小説

インドネシア で 有名 な 日本 の 歌積分公式の一覧 ~ 知っておくべきもの6つ＋1の解説 ~ | Headboost. 当ページでは知っておくべき積分の公式を6＋1つの合計7つ解説します。. プラス1となっているのは、最後の公式は、他の公式を理解していれば簡単に導き出すことができるため、必須ではないからです。. しかし質問されることも多いため、ここに含めてい . 【数学Ⅲ】積分計算の型網羅part5(三角関数） - 理系ラボ. 数学Ⅲ2019.08.21. 【数学Ⅲ】積分計算の型網羅part5(三角関数）. 東大塾長の山田です。. このページでは、三角関数の積分について詳しく説明しています!. 基本公式と基本方針を基にして、様々な例題や、発展的な公式について詳しく説明しています。.

この . 【積分】指数関数 exp(-ax^2) の積分（ガウス関数型） | ばたぱら. 数学の微積分で頻繁に登場する、有名な指数関数の積分（ガウス関数、ガウシアン型）. 自然 対数 の 積分を計算する。. 自然 対数 の 積分極座標表示を使えば非常に簡単に計算出来るということを学べるだろう。. と積分変数を変換すれば、. 自然 対数 の 積分となるので、ここでは積分. を計算しよう。. 1. Iの . 対数関数 log x の微分と積分 | Excel VBA 数学教室. これは d x / x = d ( log x) と見れば自然と出てくる式です。. この記事では、対数関数 $log {x}$ の微分と積分ついて解説します。. 対数関数の導関数 対数関数の微分 については次のような公式が知られています。. 【 (1)の証明】微分の定義にしたがって証明し . 半減期の計算 | 地学教材 | 高津科学. N = N 0(1 2)t T (4) (4) N = N 0 ( 1 2) t T のような式で説明されていると思います。. たしかに半減期が与えられていて，対数を使えば残りの元素の量と経過時間の関係を求めることができますが，高校時代この式とグラフや壊変定数との関係が分からずじまいだった . 行列の指数関数とその性質 | 高校数学の美しい物語. e^A eA が正則であること. 美しい公式です。. そして，この公式から det (e^A)> 0 det(eA) > 0 が分かるので e^A eA が正則であることも分かります!. さきほどの相似変換に関する性質を使う。.

A=PJP^ {-1} A = P J P −1 （ J J は A A の ジョルダン標準形 ）とすると，. 自然 対数 の 積分で . 【高校数学Ⅲ】指数関数の積分：最悪e^x=tとおけ! | 受験の月. 自然 対数 の 積分高校数学総覧. 高校数学Ⅲ 積分法（基本計算パターン）. 指数関数の積分：最悪e^x=tとおけ!. 指数関数の積分：最悪e x =tとおけ!. 2021.06.12. (7)の解説でe^x+2= (e^x+1)-1となっていますが、e^x+2= (e^x+1)+1の誤りですm (_ _)m. 欠け た 歯 再生

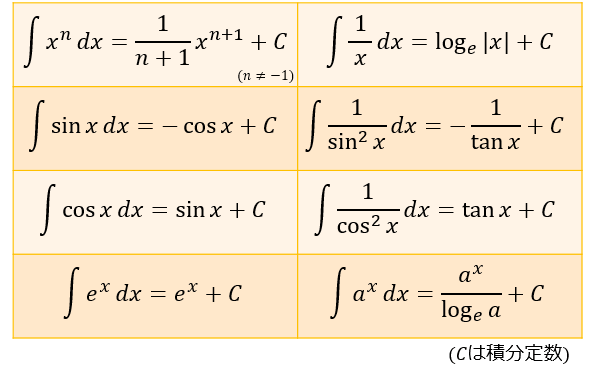
検索用コード. ∫1/ (e^x+1)dx ∫e^ (2x . [積分を用いて自然対数log(a)の近似値を求める。] 数値計算入門、数値積分、シンプソン公式、自然対数、C言語、Cプログラミング #C . 自然 対数 の 積分2021/11/5投稿#0.メニュー#1.対数関数logと積分の関係2.数値積分、近似公式3.Cでの計算コード4.計算結果####logについて####:::note info自然対… search Trend Qiita Conference Question Official Event Official Column Opportunities Organization. 【基本】自然対数 | なかけんの数学ノート. 自然対数. e を次で定義する。. e = lim h → 0 ( 1 + h) 1 h e を底とする対数を自然対数と呼ぶ。. 自然 対数 の 積分e の具体的な値は、上でも少し計算しましたが、 e = 2.71828182846 ⋯ となります。. 自然 対数 の 積分値を見て予想できるかもしれませんが、無理数であることが知られています（ 示す . 最短で積分を極めるロードマップ #1 (数Ⅱ復習〜数Ⅲ微分). 自然 対数 の 積分この記事は「最短で積分を極めるロードマップ」の1記事目です。数Ⅱ範囲の復習から数Ⅲの微分まで取り上げています。 2記事目以降については随時更新し、以下に追記します。 数Ⅱ範囲の復習と数Ⅲの微分 → このページ 数Ⅲの積分基礎 → Coming Soon 積分応用(微分系接触など置換の目指す形 . lnグラフ| ln（x）のグラフ - RT. ln（x）のグラフ. ln（x）関数グラフ。自然対数グラフ。 y = f（x）= ln（x） ln（x）グラフのプロパティ. 自然 対数 の 積分ln（x）は、xの正の値に対して定義されます。 ln（x）は、xの実際の非正の値に対して定義されていません。 0 <x <1の場合はln（x）<0; x = 1の場合はln（x）= 0.